Module 10: Popular frameworks and toolkits

ScalaTest and ScalaCheck

Problem definition

We are going to use an example from Clustering algorithms domain to practice our testing skills. Specifically we are going to work with dissimilarity or distance measures. Dissimilarity is an important part of clustering as almost all clustering algorithms rely on some distance measure to define the clustering criteria.

The most common distance measure for continuous data is the Euclidean distance. Given two data points $\boldsymbol{x}$ and $\boldsymbol{y}$ in a $d$-dimensional space, the Euclidean distance between the two data points is defined as

$D_{euc}(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{\sum_{j = 1}^{d} \left(x_j - y_j \right)^2},$

where $x_j$ and $y_j$ are the $j$th components of $\boldsymbol{x}$ and $\boldsymbol{y}$, respectively.

A simple example for $d = 2$ (the plane), is illustrated in the following figure:

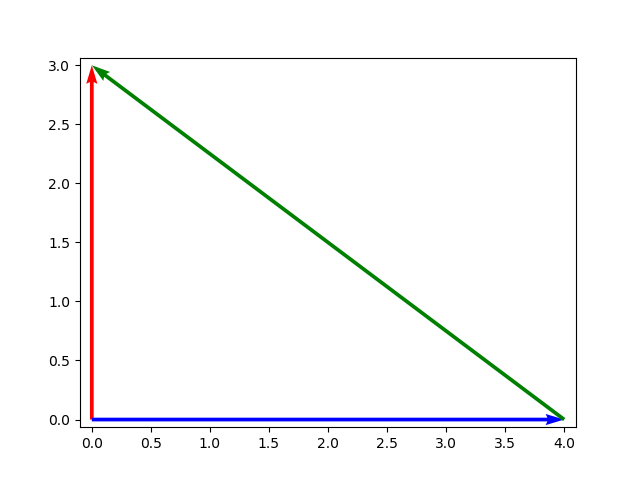
Simple Distance

for the following data:

$\boldsymbol{x} = [0, 3]^T$
$\boldsymbol{y} = [4, 0]^T$

Using the euclidean distance gives $D_{euc}(\boldsymbol{x}, \boldsymbol{y}) = 5.0$. Notice that previous formula for $d = 2$ is the simplest form of the Pythagorean theorem.

In general (Gan 2011), a distance function $D$ on a dataset $X$ is a binary function that satisfies the following conditions:

$D(\boldsymbol{x}, \boldsymbol{y}) \geq 0$ (Nonnegativity);
$D(\boldsymbol{x}, \boldsymbol{y}) = D(\boldsymbol{y}, \boldsymbol{x})$ (Symmetry or Conmutativity);
$D(\boldsymbol{x}, \boldsymbol{y}) = 0$ if and only if $\boldsymbol{x} = \boldsymbol{y}$ (Reflexivity);
$D(\boldsymbol{x}, \boldsymbol{y}) \leq D(\boldsymbol{x}, \boldsymbol{z}) + D(\boldsymbol{z}, \boldsymbol{y})$ (Triangle inequality),

where $\boldsymbol{x}$, $\boldsymbol{y}$, and $\boldsymbol{z}$ are arbitrary data points in $X$. A distance function (that satisfies the above 4 conditions) is also called a metric.

The exercise

Use Scalatest to test that the four conditions hold for Euclidean distance in the plane for the two example vectors given above.
Use ScalaCheck to test the four conditions for 100 randomly generated vectors in $\mathbb{R}^2$ (the plane in 2 dimensions!).

Scalaz ZIO

Let’s start by introducing the Scalaz ZIO’s “Hello, World!”. First, you would have to add a new dependency to your libraryDependencies SettingKey. Current version of the library, at the moment of writing is 0.3.2.

The following snippet asks for the user name, then greets the user in the console output.

package com.intersysconsulting

import java.io.IOException

import scalaz.zio.console._
import scalaz.zio.{App, IO}

object EuclideanDistance extends App {

  // Using ExitStatus.DoNotExit to be able to run this from sbt
  //   and avoid exiting from sbt
  def run(arg: List[String]): IO[Nothing, ExitStatus] =
    myAppLogic.attempt.map(_.fold(_ => 1, _ => 0)).map(_ => ExitStatus.DoNotExit)

  def myAppLogic: IO[IOException, Unit] =
    for {
      _ <- putStrLn("Hello! What is your name?") // Prints to console
      n <- getStrLn // Waits for user input
      _ <- putStrLn("Hello, " + n + ", good to meet you!") // Greets the user
    } yield ()
}

Leveraging `Refined` and Spire

The following implementation solves the problem for real vectors in 2D:

package com.intersysconsulting

import java.io.IOException

import scalaz.std.anyVal.doubleInstance
import scalaz.syntax.show._
import scalaz.zio.console._
import scalaz.zio.{App, IO}
import eu.timepit.refined._
import eu.timepit.refined.api.Refined
import eu.timepit.refined.collection.Size
import eu.timepit.refined.generic.Equal
import spire.implicits._

object Distance2D extends App {
  type S2 = Size[Equal[W.`2`.T]]
  type V2[T] = Vector[T] Refined S2
  type Error = String
  type V2Ref[T] = Either[Error, V2[T]]

  def distance2D(v1: Vector[Double], v2: Vector[Double]): Either[Error, Double] =
    for {
      _ <- refineV[S2](v1)
      _ <- refineV[S2](v2)
    } yield v1.distance(v2)

  val a1 = Vector(0.0, 3.0)
  val a2 = Vector(4.0, 0.0)

  val d1: Either[Error, Double] = distance2D(a1, a2)
  val msg = d1.fold(identity, _.shows)

  def run(arg: List[String]): IO[Nothing, ExitStatus] =
  myAppLogic.attempt.map(_.fold(_ => 1, _ => 0)).map(_ => ExitStatus.DoNotExit)

  def myAppLogic: IO[IOException, Unit] =
    for {
      _ <- putStrLn(s"Distance: $msg")
    } yield ()
}

It was necessary to add Spire as a dependency:

libraryDependencies += "org.typelevel" %% "spire" % "0.16.0"

The distance calculation is done in the for comprehension:

    for {
      _ <- refineV[S2](v1)
      _ <- refineV[S2](v2)
    } yield v1.distance(v2)

refineV[S2](v1) is equivalent to refineV[Size[Equal[W.2.T]]], by mere substitution, and given the input type, returns a V2Ref[Double] value (or equivalently, Either[String, Vector[Double] Refined Size[Equal[W.2.T]]]).

If both v1 and v2 inputs had exactly size 2, then we compute the distance between the 2 vectors using an Euclidean distance/metric.

You could try the above program, and verify that the computed output is 5.0, as expected.

Note: If the above code results too complex for you, you can always compute the distance using a Java program that implements the Pythagorean theorem.

ScalaTest

Now, let’s use ScalaTest to verify that our implementation is correct.

package com.intersysconsulting

import org.scalatest.{FlatSpec, Matchers}

class Distance2DSpec extends FlatSpec with Matchers {
  "The euclidean distance for 2D vectors v1 and v2" should "be 5.0" in {
    Distance2D.d1 shouldBe Right(5.0)
  }
}

You can run all the tests with the test sbt task. If you want to run only the tests implemented in the above Spec (Distance2DSpec), you can use the runOnly sbt task:

> runOnly com.intersysconsulting.Distance2DSpec

After running the above test with sbt, you should get a similar output:

[info] Distance2DSpec:
[info] The euclidean distance for 2D vectors v1 and v2
[info] - should be 5.0
[info] ScalaTest
[info] Run completed in 2 seconds, 270 milliseconds.
[info] Total number of tests run: 1
[info] Suites: completed 1, aborted 0
[info] Tests: succeeded 1, failed 0, canceled 0, ignored 0, pending 0
[info] All tests passed.

A closer look to the distance computation

The final computation at the end of the for comprehension v1.distance(v2) is possible only because Spire defines de following operation over MetricSpace[Vector[[Double]]:

final class MetricSpaceOps[V](lhs: V) {
  def distance[F](rhs: V)(implicit ev: MetricSpace[V, F]): F =
    macro Ops.binopWithEv[V, MetricSpace[V, F], F]
}

The code compiles because the compiler is able to provide an implicit evidence ev: Metric[V, F] for the concrete types V = Vector[Double] and F = Double. That is, Spire is able to provide an implementation that “proves” that there is a metric in the vector space of Vector[Double] that maps every pair of Vector[Double]s with a distance of type Double.

If we turn IntelliJ implicit hints on, we might realize, that the compiler is pulling a SeqNormedVectorSpace[Double, Vector[Double]] def implicit, using DoubleAlgebras.

Running the test uses the Euclidean distance metric.

Using other metrics to compute distances

We might want to provide explicitly a different metric to compute distances for vectors in $\mathbb{R}^2$. We might use the following (different) definition:

def distance2D[F](v1: Vector[F], v2: Vector[F])
  (implicit ev: NormedVectorSpace[Vector[F], F]): Either[Error, F] =
    for {
      _ <- refineV[S2](v1)
      _ <- refineV[S2](v2)
    } yield v1.distance(v2)

Again, we are only accepting 2D vectors. However, now we are using a different metric to compute the distance, because the yield expression is equivalent to:

metricSpaceOps(v1).distance(v2)(ev)

So, if we wanted to compute the maximum distance between two data points, defined as

$D_{max}(\boldsymbol{x}, \boldsymbol{y}) = \max_{1 \leq j \leq d} \left| x_j - y_j \right|$

we could simply provide a SeqMaxNormedVectorSpace metric using DoubleAlgebra:

val d2 = distance2D(a1, a2)(new SeqMaxNormedVectorSpace())

Exercise

Use Spire.std.SeqLpNormedVectorSpace with p = 1, to compute the Manhattan distance for the same pair of inputs.